Multiple linear regression in Python Tutorial

Use Multiple linear regression in python when you have more than three measurement variables and one of the measurement variables is the dependent (Y) variable.
The rest of the variables are independent (X) variables you think they may have an effect on the dependent variable.
The purpose of a multiple regression is to find an equation that predicts the Y variable as a linear function of the X variables.

Multiple linear regression example python :-

Y= b0 + b1*x1 + b2*x2 + b3*x3 +…… bn*xn
  Y = Dependent variable and x1, x2, x3 … xn =multiple independent variables

Assumption of Regression Model :-

• Linearity: The relationship between dependent and independent variables should be linear.
• Homoscedasticity: Constant variance of the errors should be maintained.
• Multivariate normality: Multiple Regressions assumes that the residuals are normally distributed.\

 

 

Lack of Multicollinearity :

It is assumed that there is little or no multicollinearity in the data.

You have to find an equation that gives a linear relationship between the X variables and the Y variable as
Ŷ=a+b1X1+b2X2+b3X3...
The Ŷ is the expected value of Y for a given set of X values. 
b1 is the estimated slope of a regression of Y on X1.
If all of the other X variables could be kept constant, and so on for b2, b3, etc.
 Not going to explain the math involved but multiple regressions finds values of b1, etc.
This can range from 0 (for no relationship between Y and the X variables) to 1 (for a perfect fit, no difference between the observed and expected Y values).
 The P value is a function of the R2, the number of observations, and the number of X variables.
When the purpose of multiple regressions is prediction the important result is an equation containing partial regression coefficients.
If you had the partial regression coefficient and measured the X variables you could plug them into the equation and predict the corresponding value of Y.
The magnitude of the partial regression coefficient depends on the unit used for each variable so it does not tell you anything about the relative importance of each variable.
When the purpose of multiple regressions understand functional relationships the important result is an equation containing standard partial regression coefficient like this-
Y'̂=a+b'1x'1+b'2x'2+b'3x'3...
Where b'1 is the standard partial regression coefficient of Y on X1.
It is the number of standard deviations that Y would change for every one standard deviation change in X1 if all the other X variables could be kept constant.
The magnitude of the standard partial regression coefficients tells you something about the relative importance of different variables X variables with bigger standard partial regression coefficients have a stronger relationship with the Y variable.

 

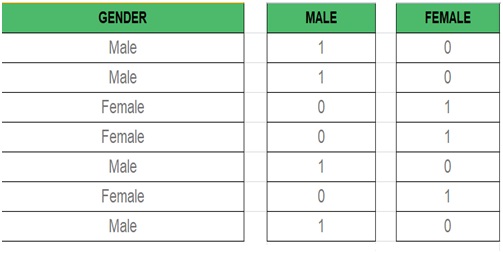
Dummy Variable –

We know in the Multiple Regression Model we use a lot of categorical data.
Using Data is a good method to include non-numeric data into respective Regression Model.
The Data will refer to data values which represent categories data values with fixed and unordered number of values for instance gender (male/female).
In the regression model, these values can be represented by Dummy Variables.
These variables consist of values such as 0 or 1 representing the presence and absence of categorical value.

Output:-

Multiple linear regression Advantages:-

• To analyzing multiple regression models first the ability is to determine relative influence of one or more predictor variable to criterion value.
• The  real estate agent could find size of homes and number of bedroom have strong correlation to price home, while proximity schools has no correlation at all.
• The example reviewing data related to management salaries the human resource manager find the number of hours worked.
• The department size and its budget all and a strong correlation to salaries.
• It would be listed predictor values and correlated to each salary being examined except one manager who has being overpaid compared to the others.

Multiple linear regression Disadvantages:-

 

• Suppose the real-estate agent is looked at only 10 homes and seven were purchased by young parents.
• In this case the relationship between schools may lead to her to believe this effect on sale price for all homes being soled in community.
• The pitfalls of in complete data she has used larger simple out of 100 homes sold.
• If she had used buyer’s age as predictor value she could found younger buyers ages as predictor value.
• She would have found youngster’s buyers were willing to pay more for homes in community of older buyers.